考虑摩擦及固态到液态相变的海底颗粒流两相两点MPM建模

摘要

精确建模海底颗粒流对滑坡灾害评估至关重要. 现有的数值方法虽关注海底滑坡的大变形特征和流体‐土体耦合, 但通常忽略了土壤的非线性固‐液相变以及对摩擦边界的合理处理. 为弥补这些不足, 本研究提出一种新型两相两点物质点法(MPM)模型, 可显式解析颗粒固‐液相变及摩擦边界. 开发的MPM框架采用两组拉格朗日物质点, 严格耦合土壤和水, 有效捕捉复杂的土‐水相互作用. 首次在两相两点MPM中引入弹塑性‐μ(I)相变模型, 以考虑颗粒从类固态到类流态的相变过程. 此外, 将摩擦接触算法引入MPM以表示摩擦边界. 为验证所提方法在模拟海底颗粒流方面的有效性, 分析了三个基准案例, 包括一个具有解析解的一维固结问题和两个实验性水下滑坡案例. 模拟结果与解析解及实验结果高度一致, 验证了模型的有效性. 特别地, 本研究对比了弹塑性‐μ(I)相变模型与纯固态弹塑性模型, 并利用提出的MPM模型评估了摩擦边界对海底滑坡的影响. 数值结果表明: (i)纯弹塑性模型相较于弹塑性‐μ(I)模型倾向于高估滑坡滑动距离; (ii)增加基底摩擦不仅显著减少土体滑动距离, 还能抑制流体涡旋, 从而削弱土‐水相互作用系统中的波浪.

研究背景

海底滑坡是海洋环境中最为复杂和最具破坏性的地质灾害之一. 历史教训惨痛: 1929年格兰德滩滑坡切断了600公里外的通信电缆; 1998年巴布亚新几内亚滑坡引发15米高海啸, 吞噬2200多条生命. 准确预测海底滑坡的动态行为, 对保障海洋工程设施安全和沿海社区防护至关重要.

存在的问题

问题一：固-液相变行为缺失

海底滑坡经历典型的“启动—运移—沉积”三阶段（图1）。在启动阶段，不稳定斜坡上的颗粒材料从固态转变为流体态；运移阶段，失效的颗粒体以流体态大规模运移；沉积阶段，材料重新恢复固态。这一复杂的相变过程在传统数值模型中被完全忽略——通常只采用单一的纯弹塑性模型或纯流体模型，无法捕捉材料状态的关键转变。

问题二：边界条件过度简化

多数模型将边界条件简化为无摩擦或完全黏着，忽略了实际滑坡体与海底之间的复杂摩擦作用，导致预测结果偏离实际。

创新解决方案：考虑摩擦边界和相变的两相两点MPM框架

文章研究创新性地提出了考虑摩擦边界和相变的两相两点物质点法（MPM）模型，这一框架具有三大核心创新：

创新一：双拉格朗日物质点系统

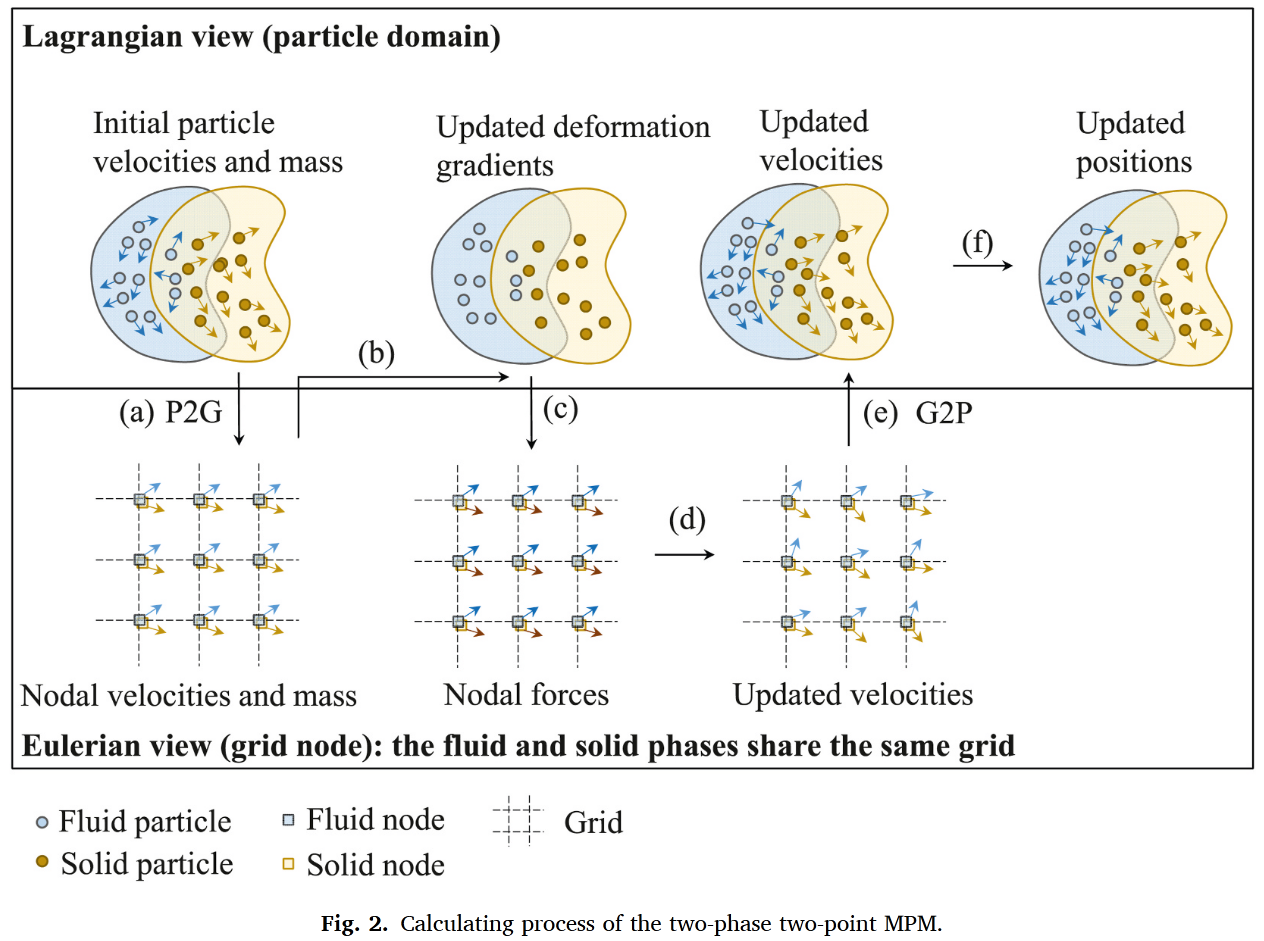
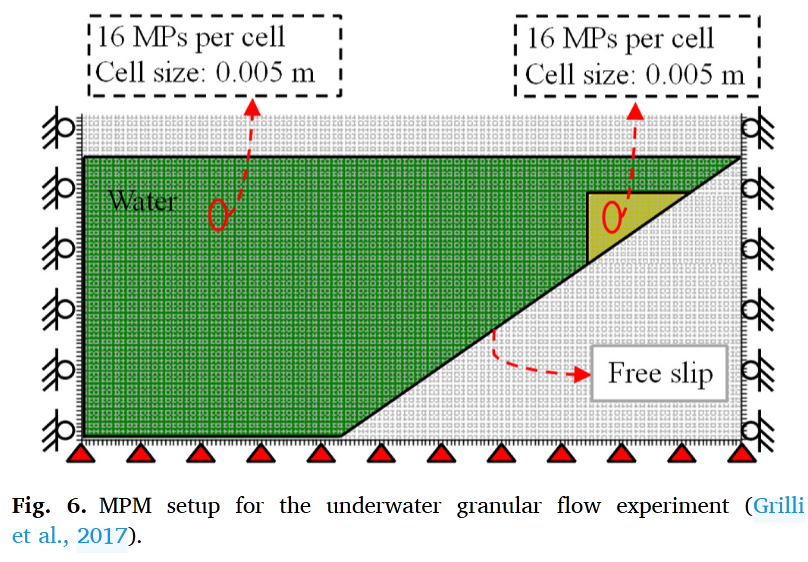
采用两套独立的物质点分别代表土体骨架和孔隙水，精确捕捉复杂的土-水相互作用机制（图2）。

创新二：弹塑性-μ(I)相变本构模型

首次将率无关的弹塑性应力（表征固态行为）和率相关的黏性应力（表征流体态行为）通过叠加方式结合，实现从固态到流体态的无缝过渡。该模型通过等效塑性应变和等效剪切粘度两个关键变量，清晰揭示材料在不同阶段的力学响应。

创新三：摩擦接触算法

引入基于库仑摩擦的接触算法，真实反映滑坡体与底床之间的摩擦效应。

框架理论

1. 控制方程

固体骨架和液相的质量守恒方程表示为:

$\frac{d(n_s\rho_s)}{dt}=-\nabla\cdot(n_s\rho_s\mathbf{v}_s) \tag{1}$ $\frac{d(n_w\rho_w)}{dt}=-\nabla\cdot(n_w\rho_w\mathbf{v}_w) \tag{2}$

其中 $\rho_s$ 和 $\rho_w$ 分别为固体骨架和水的密度; $v_s$ 和 $v_w$分别表示固体骨架和水的速度; $n_s$为固体骨架的体积浓度; $n_w$为水的体积浓度, 也称为孔隙率。注意 $n_s+n_w=1$.

固体骨架和液相的动量守恒方程表示为:

$n_s \rho_s \dot{v}_s = \nabla \cdot \bar{\sigma}_s + n_s \rho_s b + f^i \tag{3}$ $n_w \rho_w \dot{v}_w = \nabla \cdot \bar{\sigma}_w + \nabla \cdot s_w + n_w \rho_w b - f^i \tag{4}$

其中$\bar{\sigma}_{s}$和$\bar{\sigma}_w$分别为体积平均的固相和液相应力, 分别表示为$\bar{\sigma}_s=\sigma’-(1-n_w)p_wI$和$\bar{\sigma}_w=-n_w p_wI$; $\sigma’$为太沙基有效应力; $s_w$为液相的粘性应力; $b$表示体力; $f^i$表示固‐流相互作用力, 表达式见下式：

$f^i=\frac{n_w\rho_wg}k(v_w-v_s)+\beta n_w^2\rho_w\|v_w-v_s\|(v_w-v_s)+\mathbf{\sigma}_w\nabla n \tag{5}$

其中, k是水力传导率(m/s)，表示为$k = \frac{\kappa \rho_w g}{\mu_w}$, 且$\kappa = \frac{d^2 n_w^2}{180(1 - n_w)^2}$其中$\kappa$是绝对渗透率(m³); $ \mu_w $ 表示水的粘度，$ d $ 表示土粒的直径；$\beta$ 是描述拖曳力与速度之间非线性关系的系数。

联立式(3)和式(4)得混合物方程：

$n_w \rho_w \dot{v}_w + n_s \rho_s \dot{v}_s = \nabla \cdot \sigma + \rho_m b \tag{6}$

其中$\sigma$是柯西总应力张量，表示为$\sigma = \sigma’ - p_w I$，这符合有效应力原理；$\rho_m$ 是混合物密度，表示为 $\rho_m = n_s \rho_s + n_w \rho_w$。

为了求解方程(1)-(6)，需要建立某些假设来简化这些方程。

(i) 固体骨架不可压缩，且标量场（密度和孔隙率）的梯度被忽略，即 $\frac{d\rho_s}{dt} = \nabla \rho_s = \nabla n_s = 0$。因此，固相的质量守恒可以重写为：

$\frac{dn_s}{dt} = -n_s \nabla \cdot (\mathbf{v}_s) \tag{7}$

(ii) 流体（水）为弱可压缩且标量场（密度）的梯度被忽略，即 $\frac{d\rho_w}{dt} \neq 0$，$\nabla \rho_w = 0$。因此，流相的质量守恒可以重写为：

$\frac{1}{\rho_w} \frac{d\rho_w}{dt} = -\frac{1}{n_w} [n_s \nabla \cdot (\mathbf{v}_s) + n_w \nabla \cdot (\mathbf{v}_w)] \tag{8}$

(iii) 固-流相间相互作用力（方程(5)）被简化为：

$f^i = \frac{n_w \rho_w g}{k} (\mathbf{v}_w - \mathbf{v}_s) \tag{9}$

此外，必须提出合适的固相和流相本构模型来闭合上述方程组。固体骨架使用第2.4小节详述的固-流相变本构模型进行模拟。水被视为弱可压缩材料，其本构模型可通过 $\frac{d\rho_w}{dt} = \frac{\rho_w}{K_w} \frac{dp_w}{dt}$ 表达。将此方程与方程(8)结合，水压力则由下式给出：

$\frac{dp_w}{dt} = -\frac{K_w}{n_w} [n_s \nabla \cdot (\mathbf{v}_s) + n_w \nabla \cdot (\mathbf{v}_w)] \tag{10}$

其中 $K_w$ 是水的弹性模量。

对于自由水条件，压力简化为：

$\frac{dp_w}{dt} = -K_w \nabla \cdot (\mathbf{v}_w) \tag{11}$

2. 摩擦接触算法

基于库仑摩擦的接触算法（由Nguyen等人于2023年提出）被集成到物质点法(MPM)框架中，以考虑摩擦边界的影响。该算法中切向速度由库仑摩擦定律控制，具体步骤如下：

(i) 确定切向和法向速度：

$v_{I}^{\text{nor},(k)} = \mathbf{n} \left( v_{I}^{k} \cdot \mathbf{n} \right) \tag{34}$ $v_{I}^{\text{tan},(k)} = v_{I}^{k} - v_{I}^{\text{nor},(k)} = v_{I}^{k} - \mathbf{n} \left( v_{I}^{k} \cdot \mathbf{n} \right) \tag{35}$

其中$n$为法向量；$v_I^k$为边界处的速度；$v_I^{nor,(k)}$和$v_I^{tan,(k)}$分别为法向速度和切向速度。基于公式(34)和(35)，可以计算出切向和法向速度的大小$\left| v_I^{nor,(k)} \right|$和$\left| v_I^{tan,(k)} \right|$.

滑动平面的法向量通过平面上的三个点计算得出，计算公式如下：

$e_n = \frac{\left( x_j - x_i \right) \times \left( x_k - x_i \right) }{\left\| \left( x_j - x_i \right) \times \left( x_k - x_i \right) \right\| } \tag{36}$

其中$x_i$、$x_j$和$x_k$分别为滑动平面中节点$i$、$j$和$k$的节点坐标。

(ii) 通过切向和法向速度确定切向和法向力：

$f_I^{nor,(k)} = v_I^{nor,(k)} \frac{m_I^k}{dt} \tag{37}$ $f_I^{tan,(k)} = v_I^{tan,(k)} \frac{m_I^k}{dt} \tag{38}$

其中$f_I^{nor,(k)}$和$f_I^{tan,(k)}$分别为法向力和切向力。

(iii) 确定摩擦力$f_{I}^{fti,(k)}$

当切向力的大小较小时，施加的摩擦力会完全抵抗切向运动，从而有效地将切向速度设为零。当切向力超过某个阈值(即$\mu_{fit} \left| f_I^{nor,(k)}\right|$)时，摩擦力将与法向力的大小成正比，并沿与切向力相反的方向作用。

$f_I^{fti,(k)} = -\frac{g_I^{tan,(k)} }{\left\| f_I^{tan,(k)} \right\| } min\left( \mu_{fit} \left\| f_I^{nor,(k)} \right\|, \left\| f_I^{tan,(k)} \right\| \right) \tag{39}$

其中 $\mu_{fit}$ 是基底摩擦参数；$\left| f_I^{nor,(k)} \right|$ 和 $\left| f_I^{tan,(k)} \right|$ 分别表示法向力和切向力的大小。

(iv) 通过摩擦力修正切向速度(见公式(40))。在修正边界网格处的切向速度后，直接将法向速度设为零，以防止颗粒穿透边界。

$\begin{cases} 若 : \left\| v_I^{tan,(k)} \right\| = 0 : \hat{v}_I^{tan,(k)} = 0 \\ 若 : \left\| v_I^{tan,(k)} \right\| \neq 0 : \hat{v}_I^{tan,(k)} = v_I^{tan,(k)} + \frac{f_I^{fti,(k)} }{m_I^k} dt \end{cases} \tag{40}$

其中 $\hat{v}_I^{tan,(k)}$ 是修正后的切向速度。

基底摩擦参数$\mu{fit}$主要受边界条件影响，并且可能在不同的天然滑坡场地和实验室测试案例中有所变化。对于实验室实验，$\mu{fit}$理想情况下应通过标准的基底摩擦试验确定（参见Kelenenová等人, 2020；Lin等人, 2023）。从物理意义上讲，$\mu_{fit}$的取值范围是0到1，文献中的值通常在0.2到0.8之间（参见Yu等人, 2023）。

当无法直接测量时，可以通过以下过程来标定$\mu{fit}$：(i) 首先确定土壤本构参数；然后 (ii) 在一系列$\mu{fit}$取值下，将实验得到的颗粒流结果与 MPM 模拟结果进行比较，以确定最佳参数。需要注意的是，准确确定$\mu_{fit}$仍然具有挑战性，值得在未来研究中进一步深入探讨。

3. 相变本构模型

颗粒材料表现出复杂的非线性行为，其特征是在类固体和类流体状态之间转变。为捕捉这种响应，我们在两相两点物质点法(MPM)框架中引入了弹塑性-μ(I)相变本构模型。该模型桥接了土壤力学中类固体的弹塑性应力和流体力学中类流体的粘性应力，能够无缝表征颗粒介质在破坏启动、流态化传播和沉积阶段的力学行为。

弹塑性-μ(I)相变模型采用叠加方法来描述相变机制，这与经典的统一摩擦-碰撞框架（Johnson and Jackson, 1987; Johnson et al., 1990）保持一致。在该框架中，颗粒介质的应力被分为两个部分：表示类固体行为的率无关弹塑性部分，以及描述类流体行为的率相关粘性应力。该模型通过弹塑性和粘性应力的动态演化来表征相变过程：在低应变率下，弹塑性应力占主导，表明材料处于类固体状态，此时碰撞应力可忽略不计；在高应变率下，粘性应力占优势，表明材料处于类流体状态，而摩擦应力则保持可忽略不计。

$\sigma' = \sigma_{sp} + \sigma_v \tag{41}$

其中$\sigma’$为土骨架的总有效应力张量；$\sigma_{sp}$为弹塑性应力；$\sigma_v$为粘性应力。

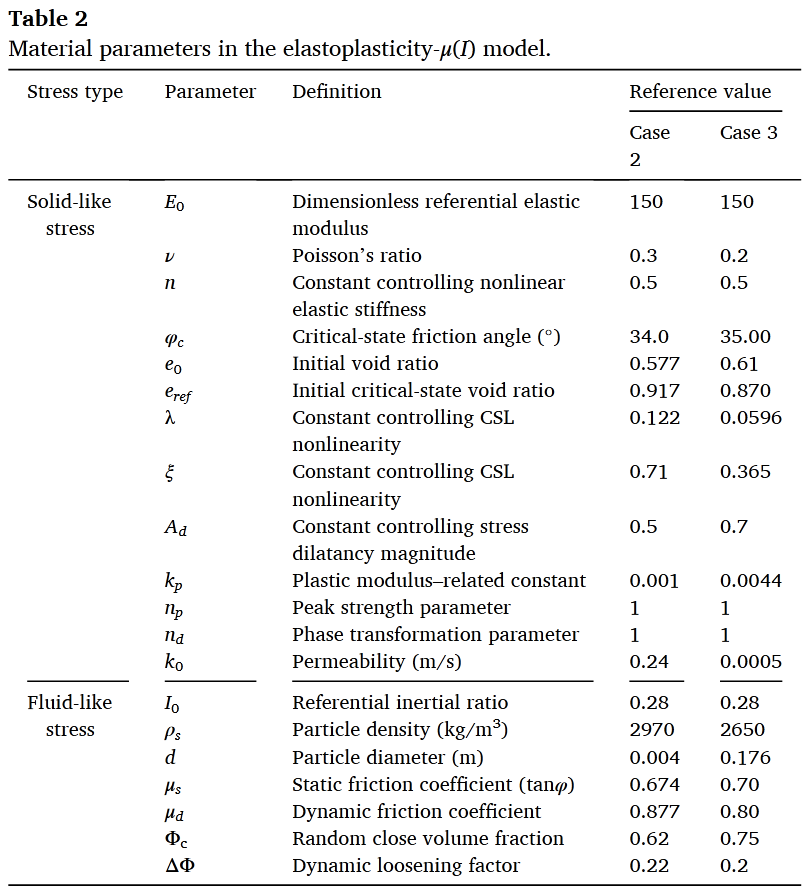
弹塑性-μ(I)模型已在我们的前期工作中进行了讨论和验证（Feng et al., ）。为清晰起见，详细的模型信息见附录A和B。关键输入参数的总结在表2中给出。

模型验证与关键发现

研究通过三个典型算例系统验证了模型的可靠性：

验证一：一维固结问题

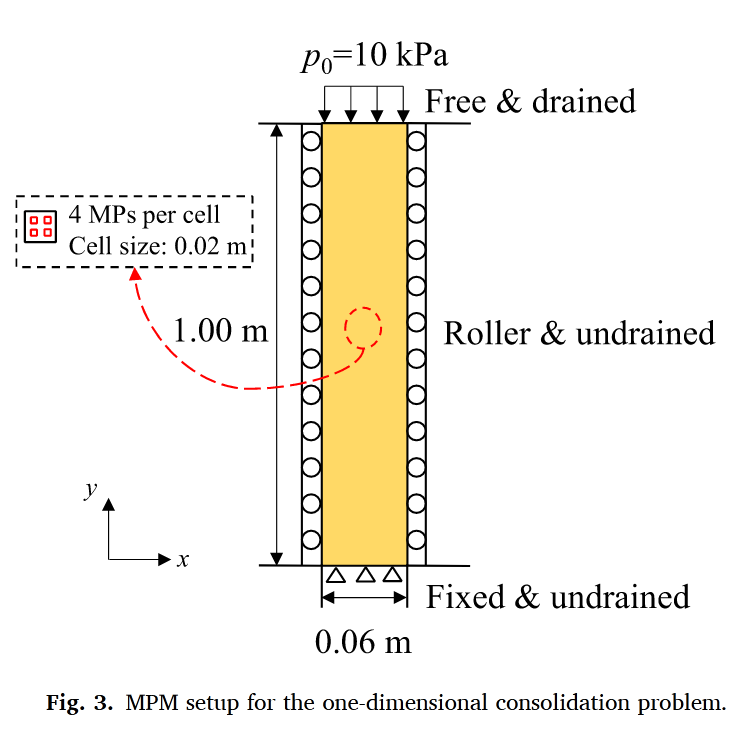
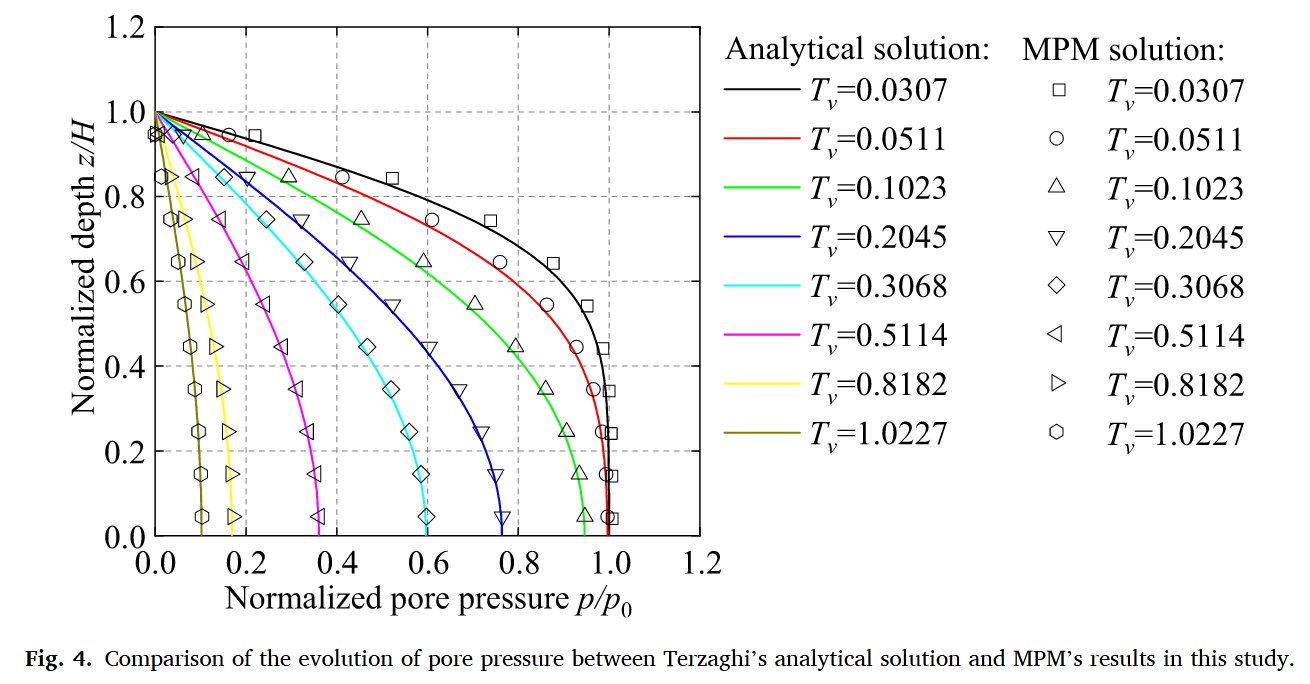
MPM计算结果与Terzaghi经典解析解高度吻合（图4），证明了模型在处理土-水耦合问题中的基本可靠性。

验证二：Grilli水下滑坡实验

模拟结果与实验观测高度一致（图7、图9）。特别值得关注的是：

相变模型准确再现了滑坡体形态演变全过程
纯弹塑性模型会系统性高估滑坡运移距离（图11、表4），因其忽略了黏性阻力
成功捕捉了由土体运动诱导的流体涡旋生成和传播过程（图10）

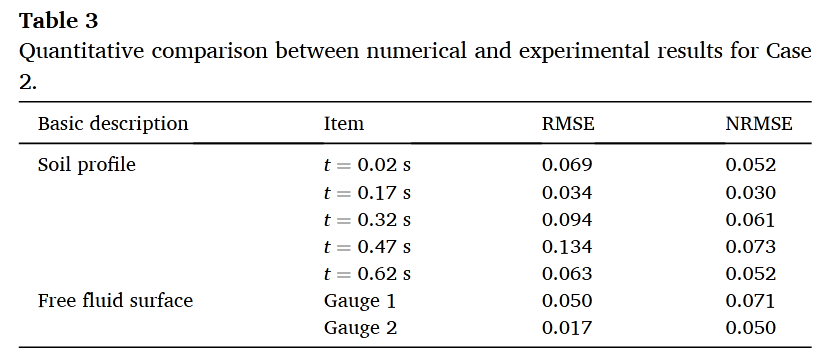
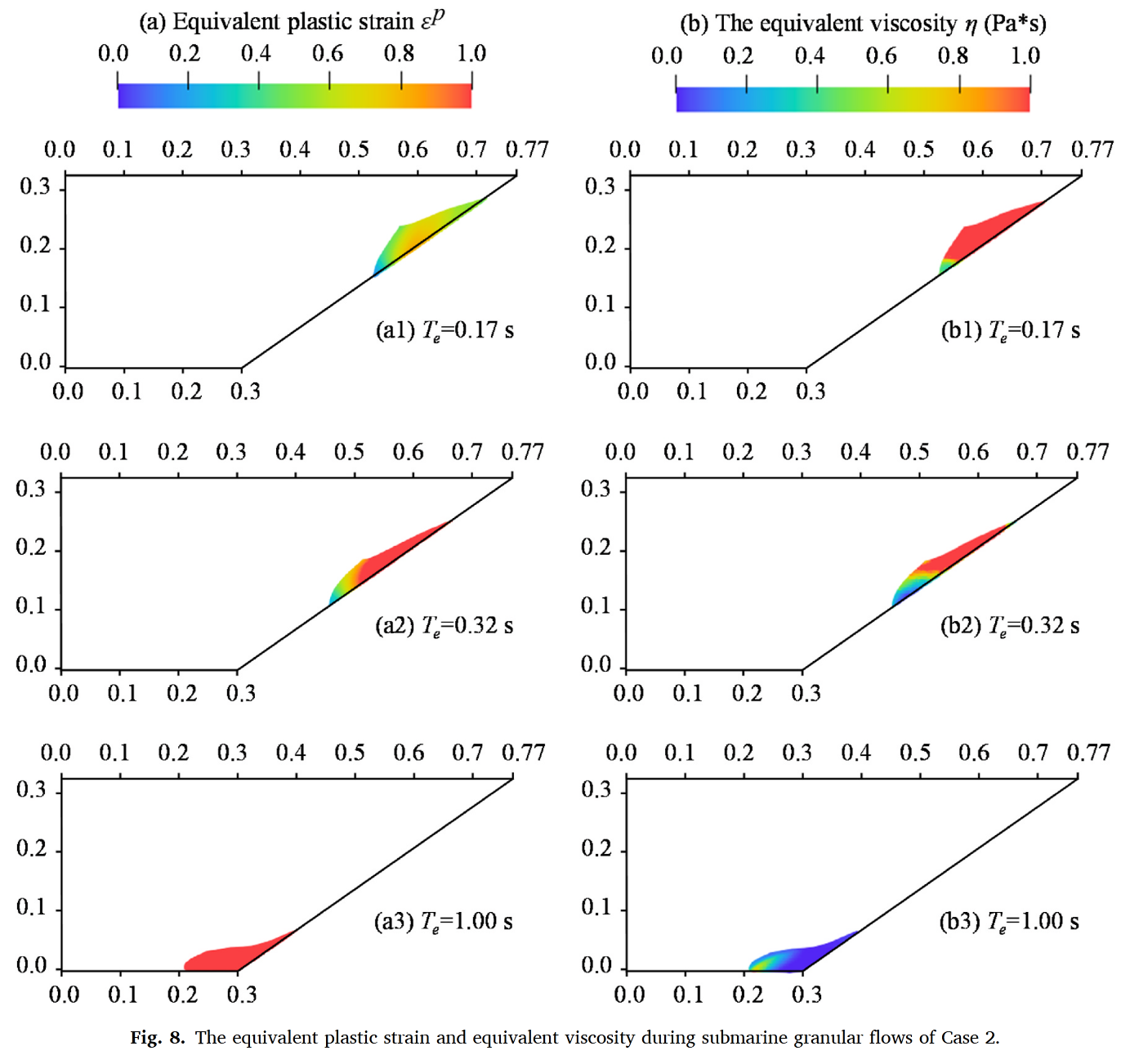
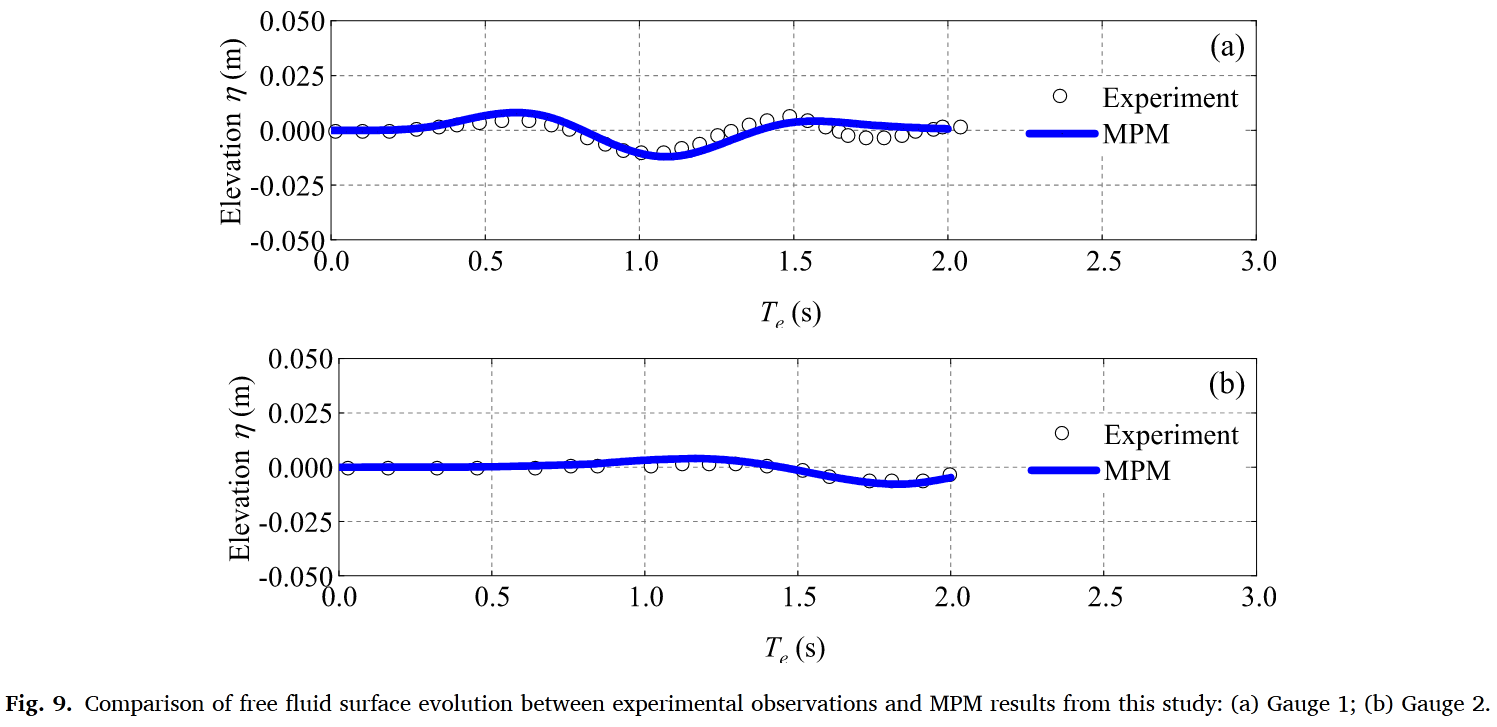
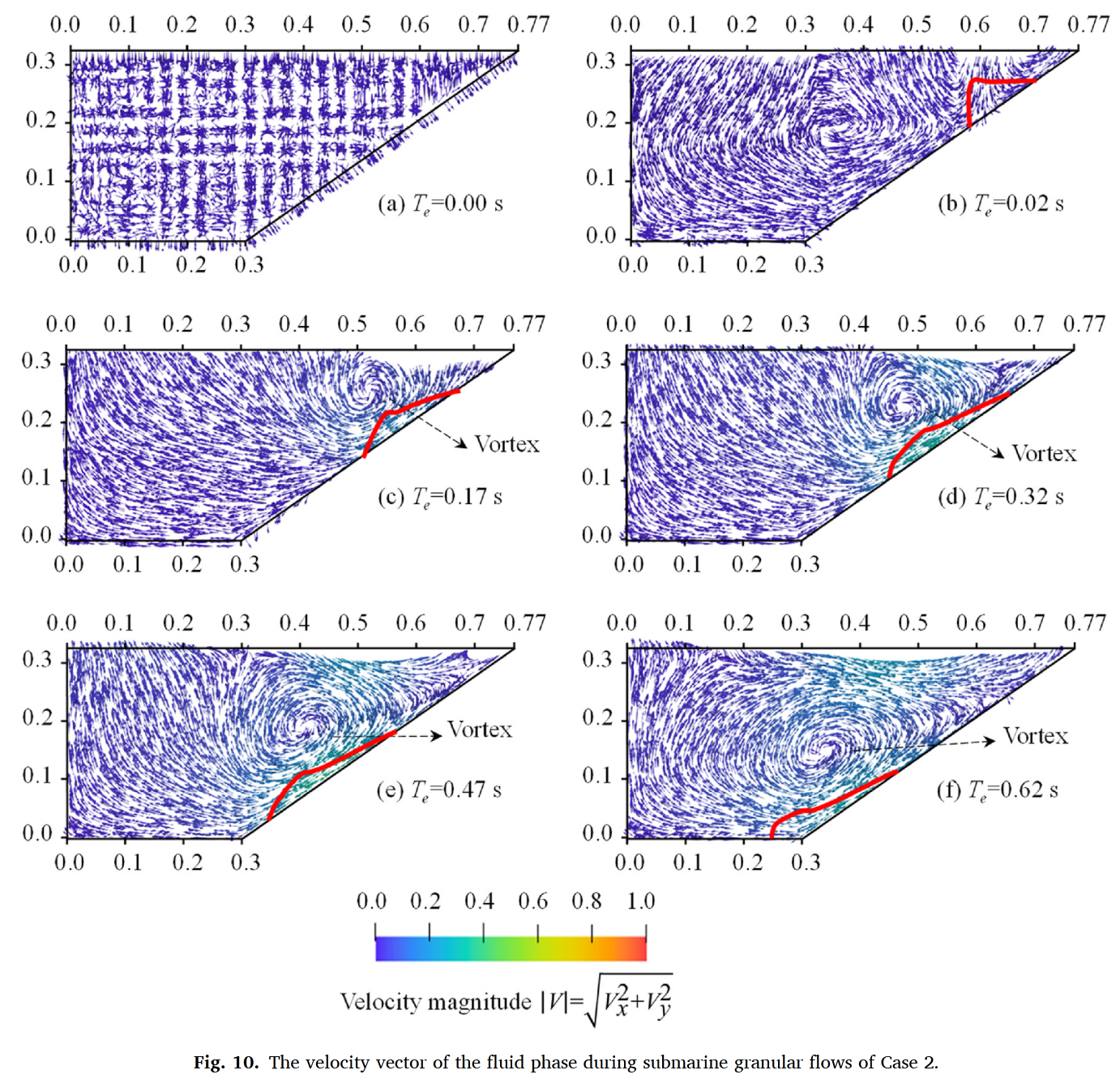
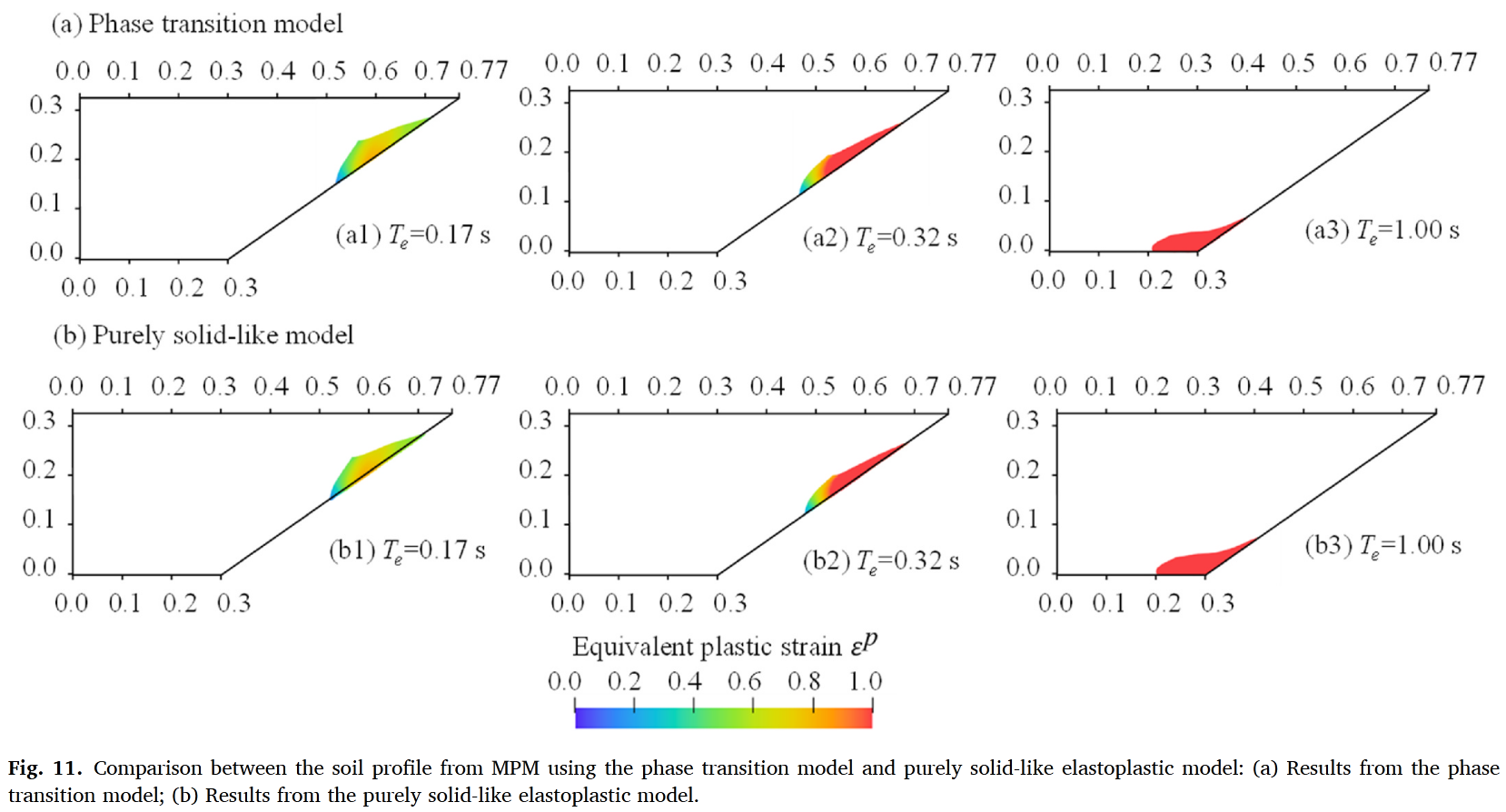
验证三：Rzadkiewicz海底滑坡实验

进一步考察摩擦边界的影响，发现：

MPM结果在土体剖面和自由水面演化方面均优于SPH和PFEM方法（图15-16、表5）
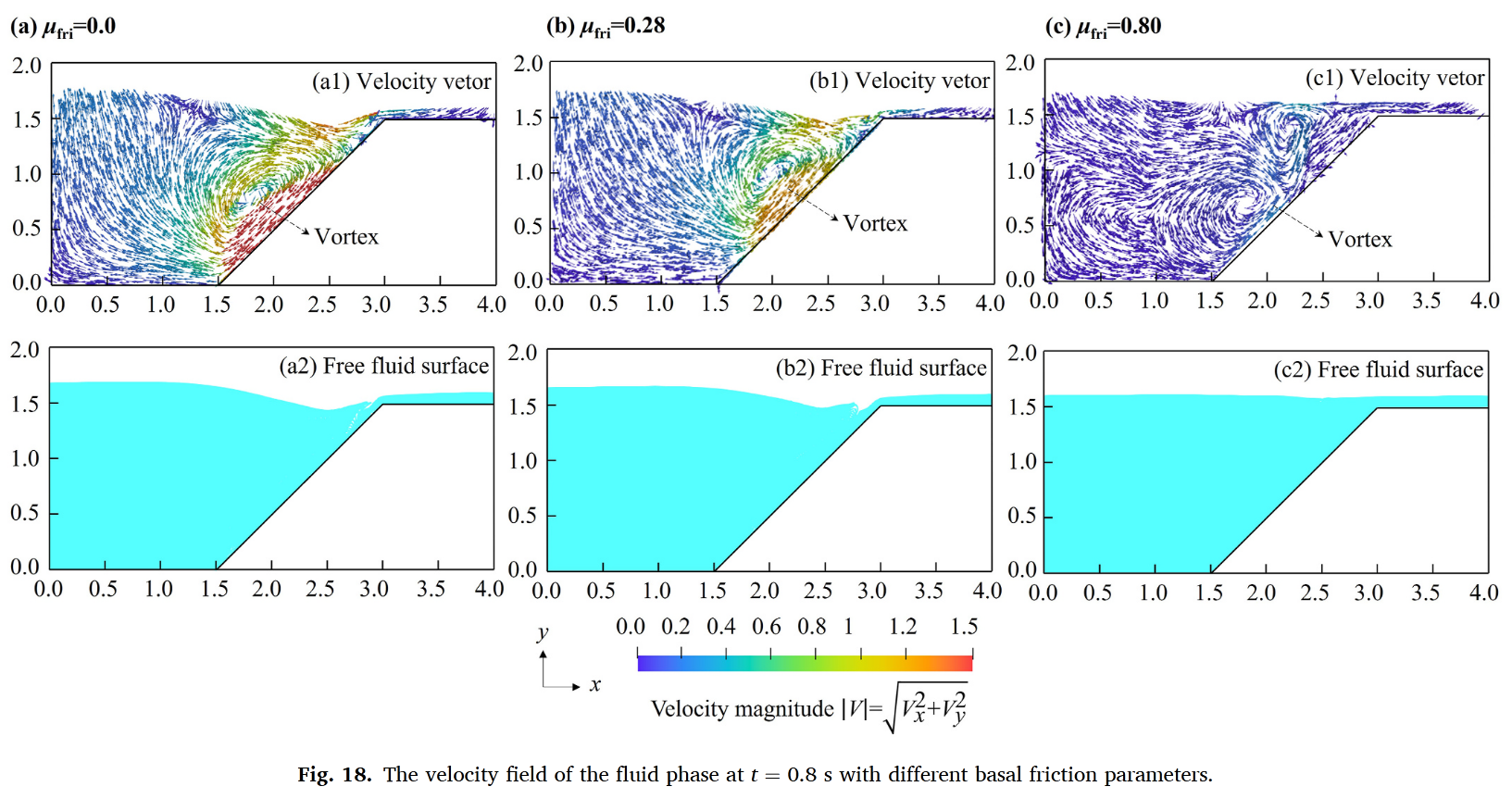
基底摩擦系数增大显著减少土体运移距离，并有效抑制流体涡旋强度（图17-18）
摩擦效应通过改变土-水界面动量传递，直接影响海啸波幅大小

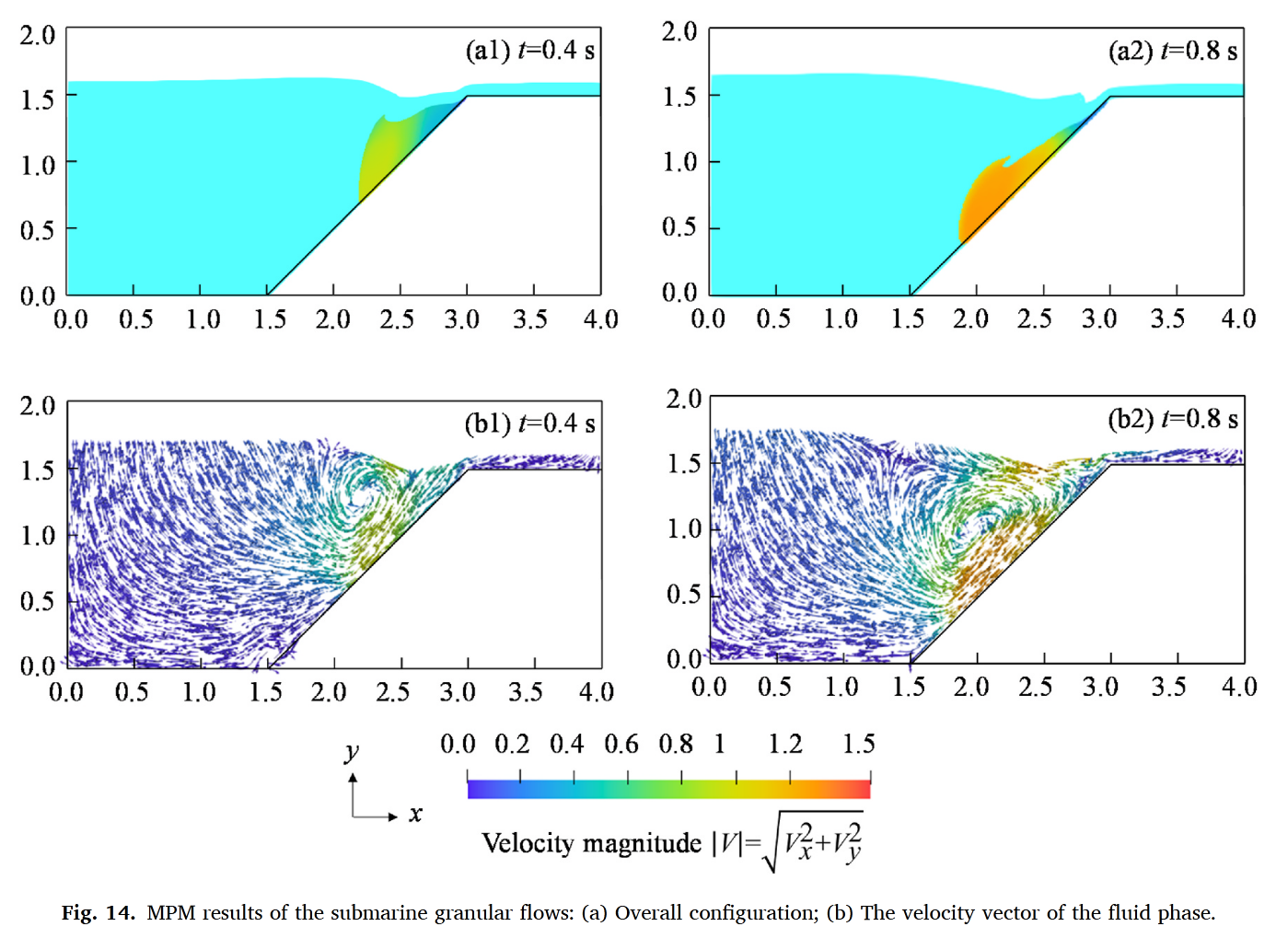
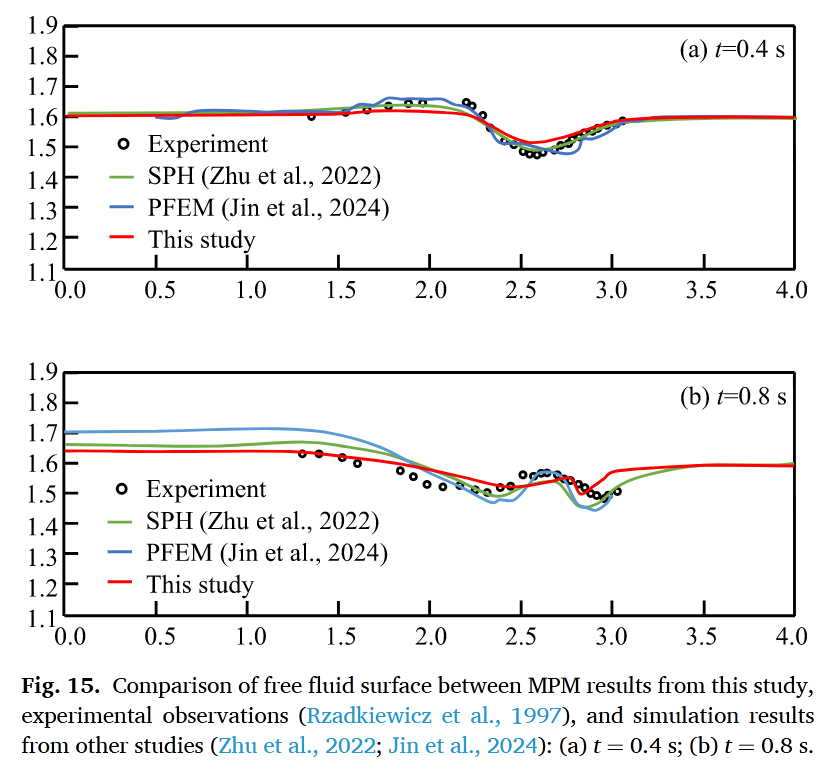
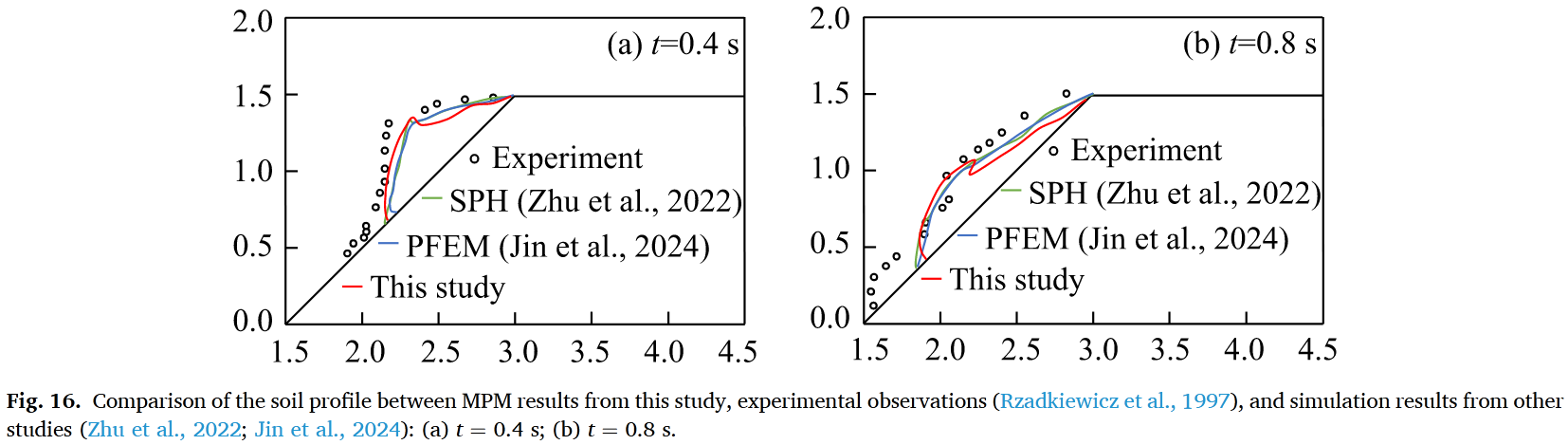
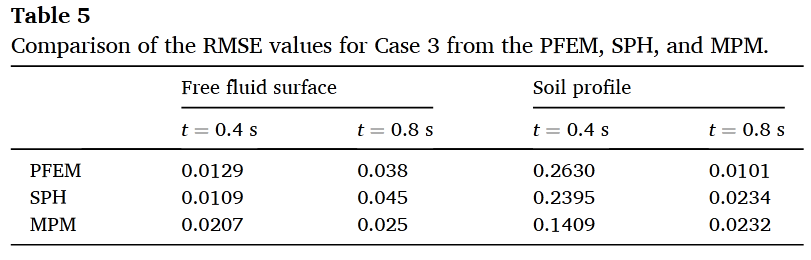
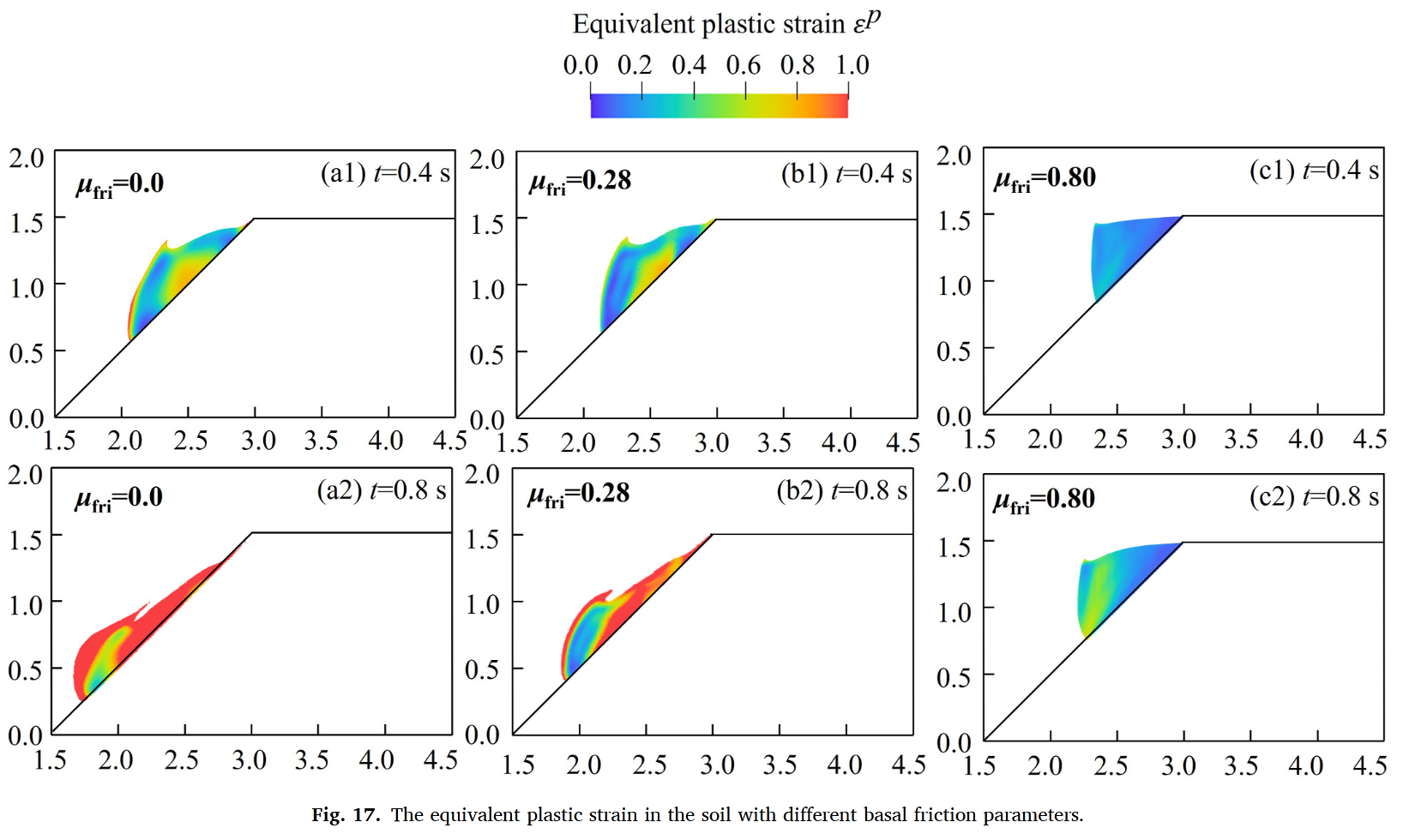
结论

文章建立的新型MPM框架，首次在考虑摩擦边界的条件下，实现了对海底颗粒流从固态到流体态全过程的精准模拟。主要结论包括：

(i) 总体而言，所提出的MPM模型的数值结果与实验数据的关键方面吻合良好，包括海底颗粒流过程、最终沉积形态和滑坡引发的海啸。虽然存在轻微差异，但该模型与大多数实验观察结果显示出良好的定性和定量一致性。

(ii) 该模型有效捕捉了海底颗粒流过程中颗粒介质的多阶段响应，其应力状态从弹塑性应力转变为弹塑性-粘性应力，并随着材料在类固体和类流体状态之间交替而恢复为弹塑性应力。

(iii) 数值结果表明，在动态的土-水系统中，颗粒介质的运动决定了流体相涡旋的方向。

(iv) 与纯类固体弹塑性模型的比较表明，纯类固体弹塑性模型往往会高估海底颗粒流的流动距离，这凸显了纳入相变机制的重要性。

(v) 不同基底摩擦参数的对比分析表明，较高的基底摩擦会减少颗粒介质的流动距离并抑制流体相涡旋，从而削弱波的形成。

本文基于 Ocean Engineering 341 (2025) 论文《Two-phase two-point MPM modeling of submarine granular flows considering solid-to-fluid phase transition over frictional plane》整理.